在看空间统计相关的文档资料的时候，看到了几个有关距离丈量方法的术语词汇，诸如：欧式距离、曼哈顿距离、切比雪夫距离…… 老外习惯于使用名字来命名算法，可是对于门外汉们，是一种困惑，今天就整理下，一起温故知新。
1. 欧式距离（Euclidean Distance）
欧式距离是我们在直角坐标系中最常用的距离量算方法，例如小时候学的“两点之间的最短距离是连接两点的直线距离。”这就是典型的欧式距离量算方法。
通常这这个距离的获取是基于我们熟悉的“勾股定理”，解算三角形斜边得到的。
看看维基百科：http://en.wikipedia.org/wiki/Euclidean_distance
2. 曼哈顿距离（Manhattan Distance）
曼哈顿距离是与欧式距离不同的一种丈量方法，两点之间的距离不再是直线距离，而是投影到坐标轴的长度之和。
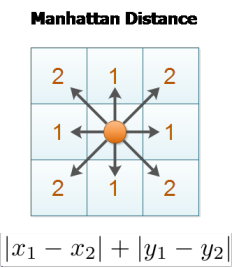
还是看图吧，图比文字更显见。
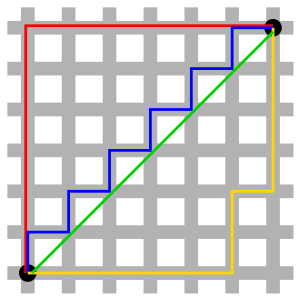
图中绿色的线为欧式距离的丈量长度，红色的线即为曼哈顿距离长度，蓝色和黄色的线是这两点间曼哈顿距离的等价长度。
想想我们下象棋的时候，车炮兵之类的，是不是要走曼哈顿距离？
如果不会下象棋，没关系，看下面的例子：
在美国道路会像这样是很多的规则的网格状，从A到B通常无法去沿直线行走，而是会避开建筑物，走几个街区到达。
图中蓝色的线即为曼哈顿距离的典型应用场景。
看看维基百科：http://en.wikipedia.org/wiki/Taxicab_geometry
3. 切比雪夫距离（Chebyshev distance）
数学上，切比雪夫距离是将2个点之间的距离定义为其各坐标数值差的最大值。
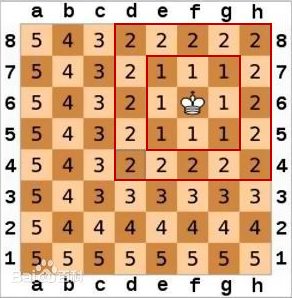
网上搜索，好多有关这个距离的解释，大多都是采用国际象棋中的王的走步来作为例子，王可以前后左右走，还可以斜前斜后走，一共8个方向可以认为距离均等。
也就是在下面3×3邻域内，中心网格的中心点到8个邻域网格中心点的距离相等。
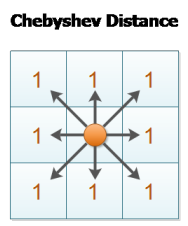
看看维基百科：http://en.wikipedia.org/wiki/Chebyshev_distance
如果您喜欢此博客或发现它对您有用，则欢迎对此发表评论。 也欢迎您共享此博客，以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权，请与作者联系以将其删除。 谢谢 ！