投影坐标系在二维平面中进行定义,投影坐标系是基于地理坐标系创建的,也就是在地理坐标系的基础上加上投影算法。
坐标原点位于网格的中心,(x,y)=(0,0)
Ⅰ 变形
地球表面是一个曲面,从曲面至平面的数学换算即为地图投影的过程,不同投影会引起不同类型的变形,例如,导致数据的形状、面积、距离或方向发生变形。
等角投影:
等角投影保留局部形状。要保留描述空间关系的各个角,等角投影必须在地图上显示以 90 度角相交的垂直经纬网线。地图投影通过保持所有角不变来加以实现。缺点是由一些弧线围起来的区域将在此过程中发生巨大变形。地图投影无法保留较大区域的形状。
等积投影:
保留所显示要素的面积。为此,形状、角和比例等其他属性将发生变形。在等积投影中,经线和纬线可能不垂直相交。有些情况下,尤其是较小区域的地图,形状不会明显变形,且很难区分等积投影和等角投影,除非加以说明或进行测量。
等距投影:
保留某些点间的距离。任何投影都无法在整幅地图中正确保持比例不变。不过,多数情况下,地图上总会存在一条或多条这样的线:比例沿着这些线将正确地保持不变。多数等距投影都具有一条或多条这样的线:在此类线中,地图上线的长度(按地图比例尺计算)与地球上同一条线的长度相同,无论它是大圆还是小圆,是直线还是曲线。此类距离被视为真实距离。例如,在正弦投影中,赤道和所有纬线就是其真实长度。在其他等距投影中,赤道和所有经线具有真实长度。而其他投影(例如,两点等距离)仍会显示地图上一点或两点与相隔点间的真实比例。请记住,任何投影都不能实现地图上的所有点是等距离的。
Ⅱ 投影方法
地图投影使用数学公式将地球上的球面坐标与平面坐标关联起来。
圆锥投影:
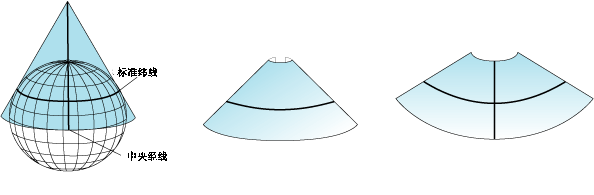
最简单的圆锥投影是沿一条纬线与地球相切获得的投影。这条纬线称作标准纬线。所有的经线都投影到圆锥面上,并在圆锥的顶点或某一点处相交。纬线在圆锥面上的投影是一个个环。将圆锥沿任意一条经线“剪开”后即可获得最终的圆锥投影,投影中的经线显示为汇聚到一点的直线,而纬线显示为许多的同心圆弧。与剪开线相对的经线成为中央子午线。
通常距标准纬线越远,变形就越严重。因此去掉圆锥的顶部会产生更精确的投影。此过程可以通过不使用极点区域的投影数据来实现。圆锥投影用于沿东西方向延伸的中纬度地区。
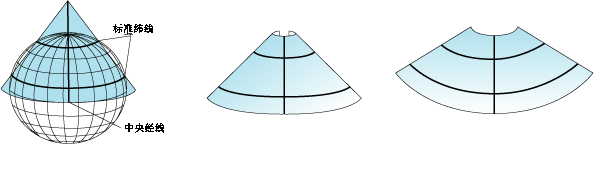
较复杂的圆锥投影会与地球表面的两处位置相接触。这类投影被称作割投影,并带有两条标准纬线。也可以使用一条标准纬线和一个比例尺因子来定义割投影。在割投影中,标准纬线之间与标准纬线之外的部分变形模式是不同的。通常,割线投影的整体变形程度小于切线投影。在更复杂的圆锥投影中,圆锥的轴并不与地球的极轴重合。此类投影称作斜轴投影。
地理要素的制图表达取决于纬线的间距。等间距排列纬线时,投影在南北方向是等距的,但不是等角或等积的。此类投影的一个示例是等距圆锥投影。对于小面积区域,整体变形是最小的。在兰勃特等角圆锥投影中,中央的纬线比靠近边缘的纬线排列得更紧密,在小比例尺和大比例尺地图中都可以保持小地理区域的形状。在阿尔伯斯等积圆锥投影中,靠近北部和南部边缘的纬线比中间的纬线更加紧密,且投影的面积不变。
圆柱投影:
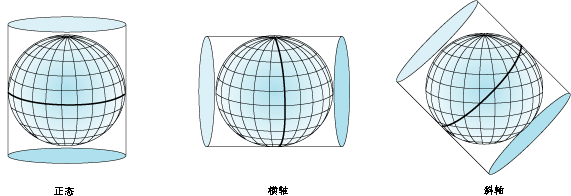
与圆锥投影类似,圆柱投影也存在相切或相割两种情况。
墨卡托投影是最常用的圆柱投影之一,并且通常以赤道为切线。经线以几何方式投影到圆柱面上,而纬线以数学方式进行投影。这种投影方式产生成 90 度的经纬网格。将圆柱沿任意一条经线“剪开”可以获得最终的圆柱投影。经线等间距排列,而纬线间的间距越靠近极点越大。此投影是等角投影,并沿直线显示真实的方向。在墨卡托投影中,恒向线、等方位角线是直线,但大多数的大圆都不是直线。
对于更复杂的圆柱投影,圆柱发生了旋转,因此切线和割线的位置发生了变化。横轴圆柱投影,例如横轴墨卡托投影,使用经线作为相切的接触线,或使用平行于经线的线作为割线。这样标准线即为南北方向的线,且其上的比例是真实的。斜轴圆柱是围绕赤道和经线间的任意大圆线旋转而成的圆柱。在此类更加复杂的投影中,大多数经线和纬线都不再是直线。
在所有的圆柱投影中,切线和割线都不发生变形,因此它们是等距离线。其他的地理属性因具体的投影方式而异。
平面投影:

平面投影将地图数据投影到与地球接触的平面。平面投影也称为方位投影或天顶投影。
此类型的投影通常在一点与地球相切,但也可能相割。接触点可以是北极、南极、赤道上的某点或者赤道与两极之间的任意点。此点会指定投影中心,并将作为投影的焦点。焦点由中央经度和中央纬度标识。可能的投影方法包括极方位投影、赤道投影和斜轴投影。
极方位投影是最简单的形式。纬线是以极点为中心的同心圆,经线是在极点处与其真实的方向角相交的直线。在其他投影方法中,平面投影在焦点处将具有 90 度的经纬网格角度。由焦点确定的方向是精确的。
穿过焦点的大圆由直线表示;因此从中心到地图上其他任意点的最短距离是直线。面积和形状变形后的图案是以焦点为中心的圆。由于这个原因,方位投影更适合圆形区域,而不太适合矩形区域。平面投影最常用于绘制两极地区的地图。
某些平面投影会在空间中从特定点来观测表面数据。观测点将确定球面数据如何投影到平面。在不同的方位投影中,用于观测所有位置的透视图也有所不同。透视点可以是地球的中心、与焦点正对的表面点或者地球外部的某点,就如同从卫星或其他星球上遥看一样。
有部分方位投影是按焦点和透视点(如果适用)分类的。球心投影从地心来观测表面数据,而立体投影是在两极之间进行观测。正射投影从无穷远点(如同从外太空)观察地球。注意观察透视图之间的差异如何决定与赤道相对的变形程度。
详情参见:http://resources.arcgis.com/zh-cn/help/main/10.2/index.html#//003r0000000p000000
ArcGIS 支持的全部投影的列表:
http://resources.arcgis.com/zh-cn/help/main/10.2/index.html#/na/003r00000017000000/
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !