空间统计(三)聚类分布制图

这组工具中包含众所周知的热点分析工具,通过这个工具我们能捕获到大量数据中的热点和冷点,对我们分析问题有很大的帮助。例如,在犯罪分析中,我们可以研究哪些位置犯罪频繁并且聚集,对增设警力有重要的辅助作用。工具集中的其他工具也有类似的作用,都是通过执行聚类分析来识别具有统计显著性的热点、冷点和空间异常值的位置。
依照惯例,我们还是 one by one 来看。
Similarity Search
相似搜索工具,顾名思义,工具根据要素属性确定哪些候选要素与输入要素最相似或者最不相似。
举个栗子:
我希望找到与圣地亚哥5岁以下儿童、未成年人、65岁以上老年人人数分布相似的城市:
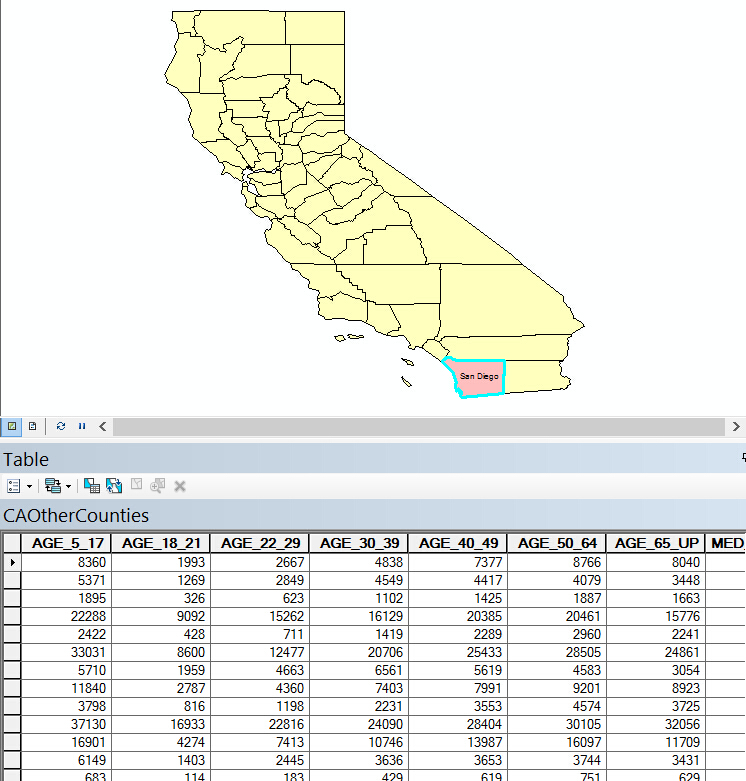
工具中我做如下配置:
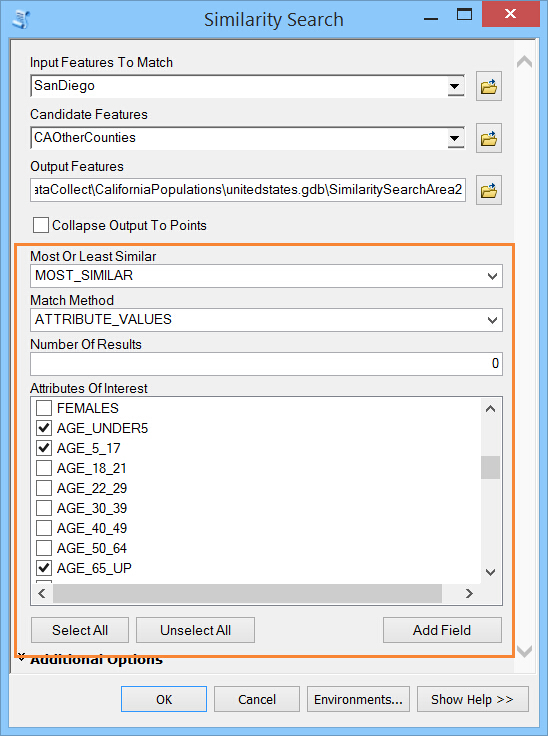
结果在这里,其中 Similarly Rank 为 1 的即为三个年龄属性最相似的城市 Orange:
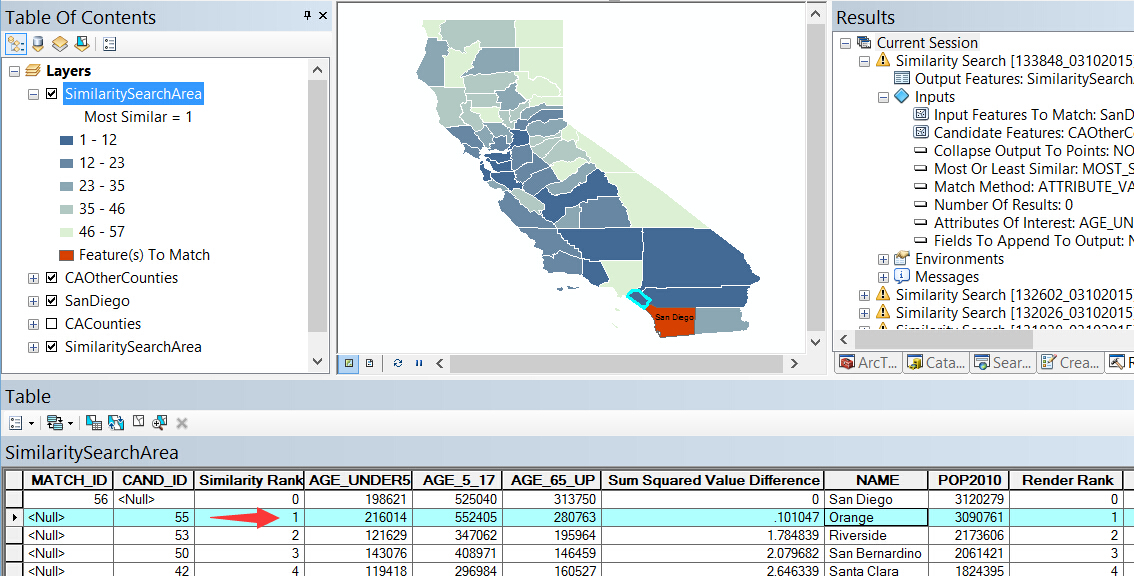
匹配方法参数中提供了3种算法,分别为:属性值、等级属性值或属性剖面(余弦相似性)。
可能的应用:
- 人力资源经理可能希望能够证明公司的工资范围。找出在大小、生活成本、市容建筑方面相似的城市后,她便可以查看这些城市的工资范围,从而查看他们是否在此行列。
- 犯罪分析师希望搜索数据库以查看某罪行是否属于较重犯罪形式或有重罪趋势。
- 课外健身计划在 A 城极其成功。计划提倡者期望找到与其计划推广的候选城市具有相似特征的其他城市。
- 执法机构用此方法揭露毒品种植地或生产地。标识具有相似特征的地方可能有助于制定未来的搜索目标。
- 大型零售商不仅拥有数个成功店铺,也有少数业绩不佳的店铺。找到一些具有相似人口特征和环境特征(交通便利性、知名度以及商业互补性等等)的地方有助于标识新店的最佳位置。
Grouping Analysis
我们在学习研究事物时,有事需要对事物进行归类从而帮助理解与分析。在ArcGIS 中,分析分组分析工具就是来进行这个逻辑分类过程,它会执行一个分类过程来查找数据中存在的自然聚类。要素相似性是基于您为分析字段参数指定的一组特性,同时还可以包括空间属性或空间-时间属性。
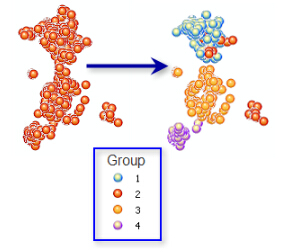
在这个工具中有个重要的参数—— Spatial Constrains,用于设置分组过程是否受某种空间关系约束,具体可选的方法如下:
- CONTIGUITY_EDGES_ONLY — 共享一条边的相连的面才属于同一个组。
- CONTIGUITY_EDGES_CORNERS — 共享一条边或一个折点的相连面才属于同一个组。
- DELAUNAY_TRIANGULATION — 同一个组中的要素至少具有一个与该组中的另一要素共用的自然邻域。自然邻域关系基于 Delaunay 三角测量。从概念上讲,Delaunay 三角测量可以根据要素质心创建不重叠的三角网。每个要素是一个三角形结点,具有公共边的结点被视为邻域。
- K_NEAREST_NEIGHBORS — 同一个组中的要素将相互邻近;每个要素至少是该组中某一其他要素的邻域。邻域关系基于最近的 K 要素,您可以在此为“相邻要素的数目”参数指定整型值 K。
- GET_SPATIAL_WEIGHTS_FROM_FILE — 空间关系和可选的时态关系通过空间权重文件 (.swm) 进行定义。使用“生成空间权重矩阵”工具创建空间权重矩阵文件。
- NO_SPATIAL_CONSTRAINT — 只能使用数据空间邻域法对要素进行分组。要素不是必须在空间或时间上互相接近,才能属于同一个组。
可能的应用:
- 假设您拥有来自所在州周围农场的沙门氏菌样本,以及包括类型/类别、位置和日期/时间在内的属性。为了更好地了解细菌如何传播和扩散,您可以使用分组分析工具将样本划分为各个“爆发”。您可能决定使用空间-时间约束,因为同一次爆发的样本会在空间和时间上会非常接近,而且也会与相同类型/类别的细菌关联。确定分组之后,可以使用其他空间模式分析工具,比如标准差椭圆、平均中心或近邻来分析每一次爆发。
- 如果您收集了有关动物观察方面的数据,以便更好地了解它们的领地,分组分析工具可能很有帮助。例如,了解鲑鱼在不同生命阶段的聚集地点和时间,可以帮助您规划保护区,以帮助确保成功繁育。
- 作为一名农学家,您可能想将研究领域内的不同土壤进行分类。对通过一系列样本发现的土壤特征使用分组分析可以帮助识别出明显的、空间上相邻的土壤类型的聚类。
按购买方式、人口统计特征和/或旅行方式对客户进行分组,可以帮助您为公司产品制订有效的营销策略。- 城市规则师常常需要将各个城市划分成不同的邻域,以便有效地定位公共设施、促进地方能动性和提高社区参与度。对城市街区的物理和人口统计特征使用分组分析,可以帮助规划师确定具有相似物理和人口统计特征并且在空间上相邻的城市区域。
- 每当对聚合的数据进行分析时,生态谬误都是一个众所周知的统计推断问题。通常,用于分析的聚合方案对我们想要分析的内容没有任何关系。例如,人口普查数据是根据人口分布而聚合,而人口分布情况可能不是用来进行火灾分析的最佳选择。针对与目前分析问题准确相关的一组属性,将可能的最小聚合单位划分成同质区域,是降低聚合偏差和避免生态谬误的一种有效方法。
Hot Spot Analysis (Getis-Ord Gi)*
热点分析工具是个 Most Popular 工具,经常会被用到,通过此工具,我们可以来识别有统计显著性的热点和冷点。例如,警察局会调查哪个区域是刑事案件的高发区?这就是一个典型的热点分析例子。如下图,黑点表示报警位置,其中属性表中包含一个报案次数的字段,得到了犯罪热点。从而警察局可以考虑在热点位置增设警力。
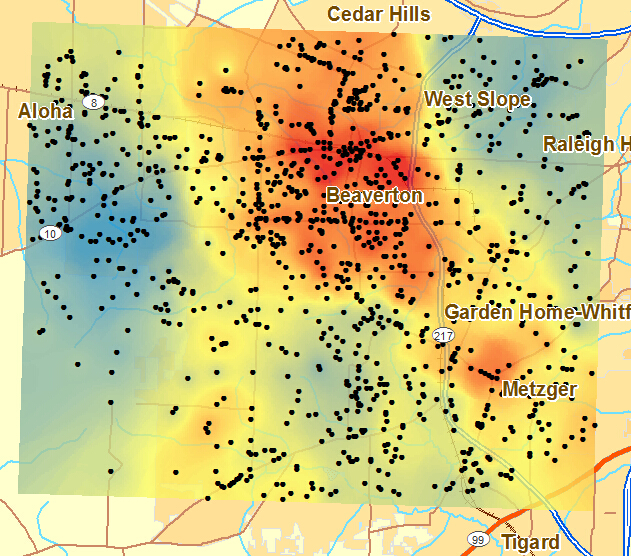
此工具的工作方式为:查看邻近要素环境中的每一个要素。因此,仅仅一个孤立的高值不会构成热点,说白了就是,单个要素以及它的邻居都是高值才算是热点。在热点分析工具中,z 得分和 p 值都是统计显著性的度量,用于逐要素地判断是否拒绝零假设。置信区间(Gi_Bin字段) +3 到 -3 中的要素反映置信度为 99% 的统计显著性,置信区间 +2 到 -2 中的要素反映置信度为 95% 的统计显著性,置信区间 +1 到 -1 中的要素反映置信度为 90% 的统计显著性;而置信区间 0 中要素的聚类则没有统计学意义。
如果要素的 z 得分高且 p 值小,则表示有一个高值的空间聚类。如果 z 得分低并为负数且 p 值小,则表示有一个低值的空间聚类。z 得分越高(或越低),聚类程度就越大。如果 z 得分接近于零,则表示不存在明显的空间聚类。
关于此工具的建议:
- 输入要素类是否至少包含 30 个要素?如果少于 30 个要素,则结果不可靠。
- 您选择的空间关系的概念化是否合适?对于此工具,建议使用固定距离范围方法
可能的应用:
- 应用领域包括:犯罪分析、流行病学、投票模式分析、经济地理学、零售分析、交通事故分析以及人口统计学。其中的一些应用示例包括:
- 疾病集中爆发在什么位置?
- 何处的厨房火灾在所有住宅火灾中所占的比例超出了正常范围?
- 紧急疏散区应位于何处?
- 峰值密集区出现于何处/何时?
- 我们应在哪些位置和什么时间段分配更多的资源?
Optimized Hot Spot Analysis
在最近几个版本的 ArcGIS 中多了一个 “优化的热点分析工具”,我们如何理解这个工具呢?打个比方,好比“数码相机自动根据光线、拍摄主体与背景对比度的读数,来确定合适的光圈、快门速度和焦点”,优化的热点分析是根据输入数据的特征派生参数,从而获得产生最佳热点结果的设置,然后执行热点分析工具。
简而言之,如果拿到单反,使用“优化的热点分析工具”好比把拍照模式调成了“全自动”,而使用“热点分析工具”好比把拍照模式调成“手动”,热点分析工具允许我们完全控制所有参数选项。运行优化的热点分析工具并记录其使用的参数设置,有助于优化设置热点分析 (Getis-Ord Gi*) 工具的参数。
打开这个工具,我们会发现,这个工具太可爱了,除了输入和输出参数,其他所有参数都是可选的,都可以不填! 果然是全自动模式,傻瓜相机版热点分析。但是,这几个参数决定了优化热点分析的方式,为了“照片”更美,还是需要了解些东西的,一起来看看:
分析字段:当要分析的数据中存在一个字段存储了采样值,我们想了解这个采样值的高值与低值的聚集区域,那分析字段就需要选择这个字段。
当我们的数据不具有这样的采样值,并且我们希望研究的是点的计数,也就是研究:哪里存在很多点?哪里存在很少点?这时,选择一种聚合方案就变得重要了。
工具中提供了三种聚合方案:
1) COUNT_INCIDENTS_WITHIN_FISHNET_POLYGONS:采用渔网聚合,渔网的网格大小由工具根据点的距离关系决定。
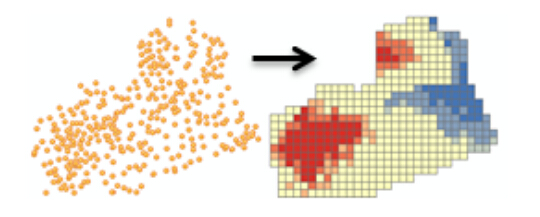
2) COUNT_INCIDENTS_WITHIN_AGGREGATION_POLYGONS:提供聚合面以覆盖事件聚合面参数中的事件点数据。计算每个面内的事件数。例如:计算加州每个城市的消防站的聚集情况。
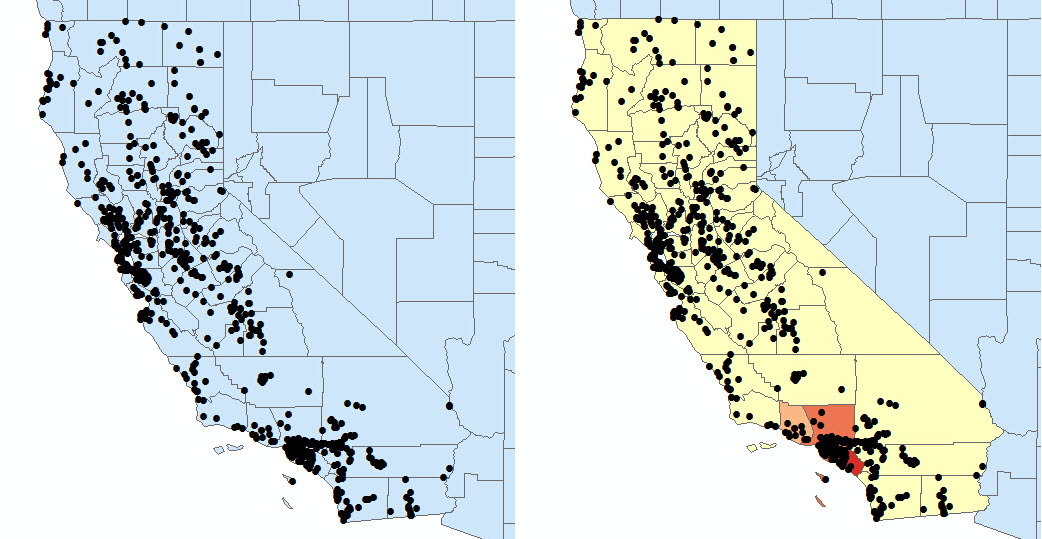
3)SNAP_NEARBY_INCIDENTS_TO_CREATE_WEIGHTED_POINTS:邻近事件将聚合在一起,从而创建单个加权点。各点的权重值是该位置的聚合事件数。
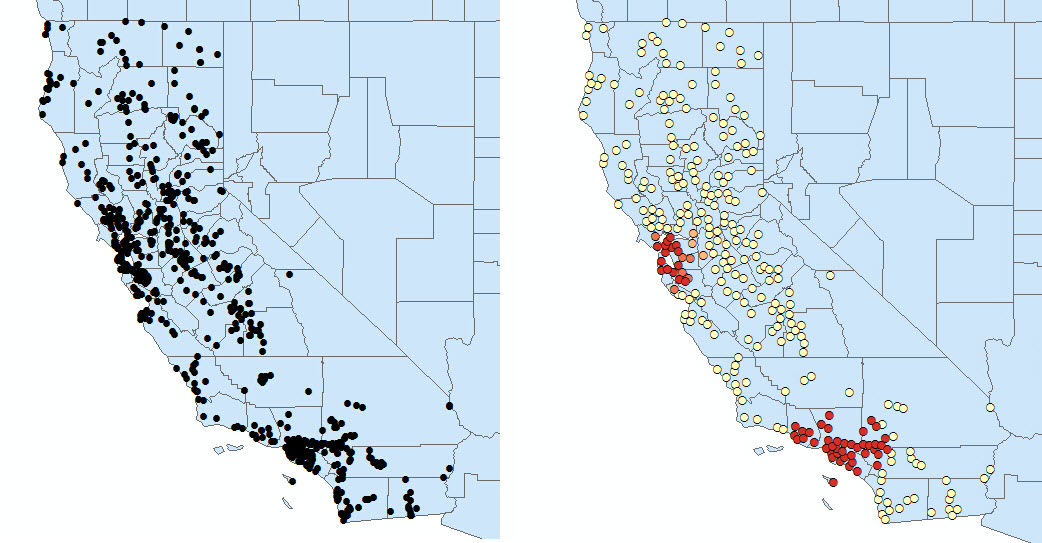
无论是哪种方法,在工具的日志中会提供一个研究这些数据聚类的最优的距离,类似:
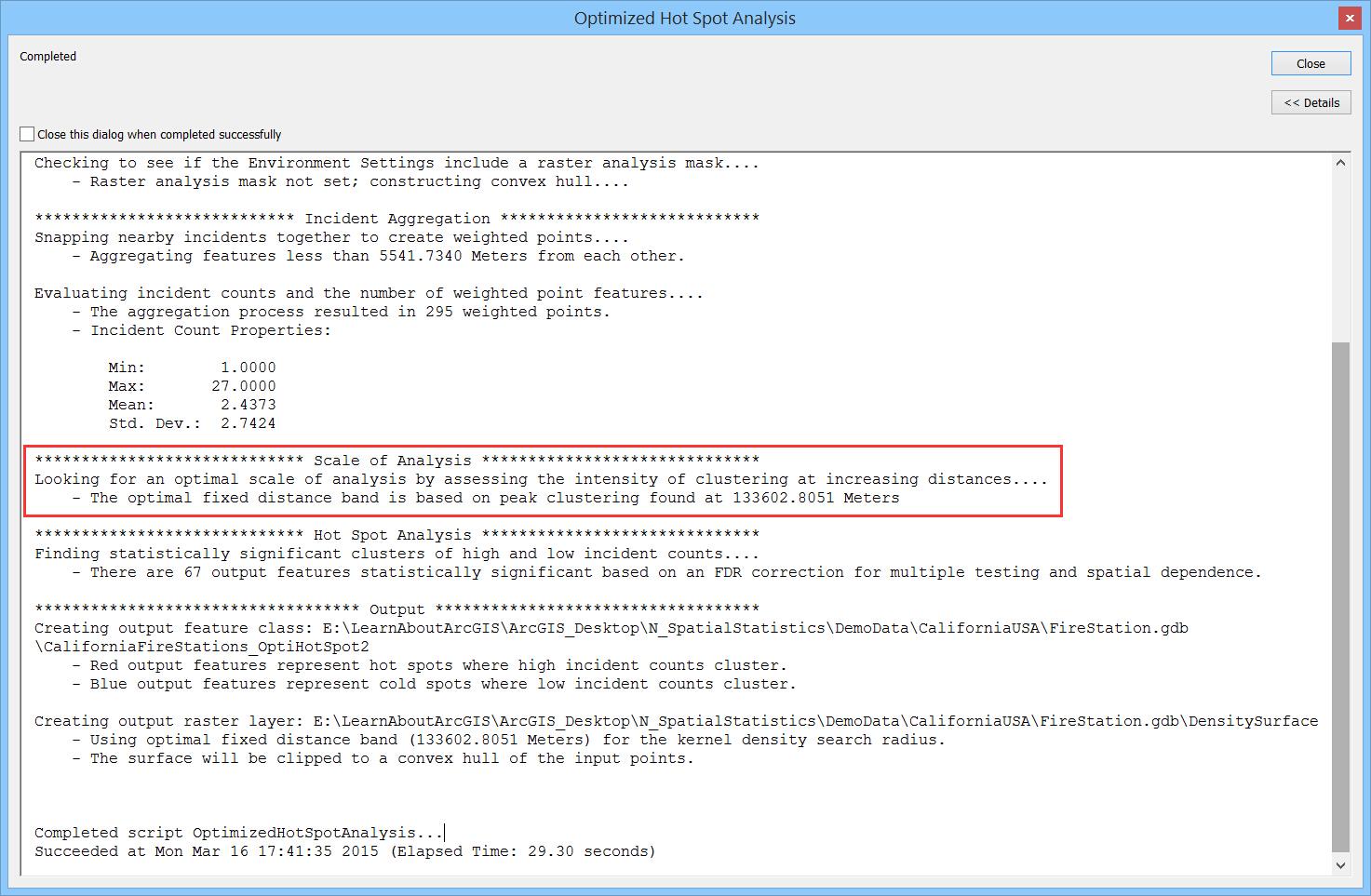
Cluster and Outlier Analysis (Anselin Local Moran’s I)
给定一组加权要素,使用 Anselin Local Moran’s I 统计量来识别具有统计显著性的热点、冷点和空间异常值。
热点分析(Getis-Ord Gi*) 工具也是查找热点和冷点位置的有效工具。但是,只有聚类和异常值分析(Anselin Local Moran’s I) 工具可以识别具有统计学上的显著性的空间异常值(高值由低值围绕或低值由高围绕的值)。
输出要素类中包含:**Local Moran’s I 指数、z 得分、p 值、聚类/异常值类型 (COType)**。
如果要素的 z 得分是一个较高的正值,则表示周围的要素拥有相似值(高值或低值)。输出要素类中的 COType 字段会将具有统计显著性的高值聚类表示为 HH,将具有统计显著性的低值聚类表示为 LL。
如果要素的 z 得分是一个较低的负值(如,小于 -3.96),则表示有一个具有统计显著性的空间数据异常值。输出要素类中的 COType 字段将指明要素是否是高值要素而四周围绕的是低值要素 (HL),或者要素是否是低值要素而四周围绕的是高值要素 (LH)。如下图可以帮助理解:
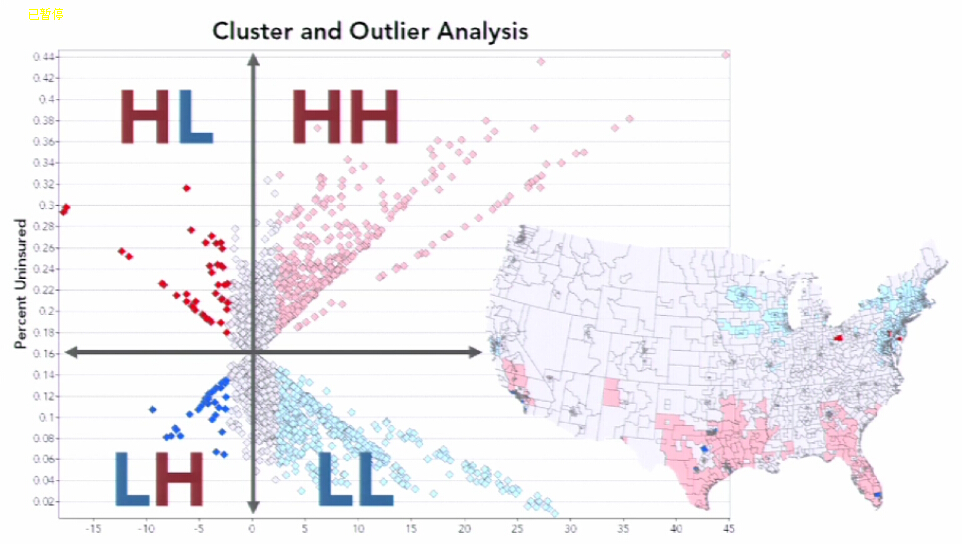
COType 字段将始终指明置信度为 95% 的统计显著性聚类和异常值。只有统计显著性要素在 COType 字段中具有值。
可能的应用
聚类和异常值分析(Anselin Local Moran’s I) 工具可识别高值密度、低值密度和空间异常值。还可帮助您解决如下问题:
- 研究区域中的富裕区和贫困区之间的最清晰边界在哪里?
- 研究区域中存在可以找到异常消费模式的位置吗?
- 研究区域中意想不到的糖尿病高发地在哪里?
可在经济学、资源管理、生物地理学、政治地理学和人口统计等许多领域中应用此工具。